【データ解析初心者必見！】データにクラスを割り当てる方法の１つ：ロジスティック回帰

f:id:wakaba-mafin:20181217154104j:plain:w180:right

得られているデータから、そのデータが属しているクラスを推定したいときってありますよね？

例えば、体調の情報から病気かどうかを判断したり、現在の湿気などから雨が降るかどうかなど...いろんな場合で考えることができます。

そんな要望に応える１つの手法がロジスティック回帰。

今回はこのロジスティック回帰についてご紹介します！

ロジスティック回帰とは
ロジスティック回帰の使い方
- STEP1:既存のデータに対する学習
- STEP2:新たなデータに対する識別
ロジスティック回帰の例
まとめ

ロジスティック回帰とは

まずはロジスティック回帰とは何たるかについてご紹介します。

ロジスティック回帰とはクラス分類と呼ばれる問題に対するアプローチの１つです。特に二クラス分類で用いられます。ここでクラス分類とはある特徴量から、そのデータが属しているクラスを識別するという問題です。例えば、病院で例を挙げるのであれば、熱や咳・頭痛の有無といった特徴から風邪かどうか判別するなどです。 f:id:wakaba-mafin:20181217160228j:plain:w100:right

数式を使って表してみましょう！

今、熱や咳・頭痛の有無といった特徴ベクトルを $\phi$ （例えば

$\phi=(\mbox{体温}, \mbox{咳の有無}, \mbox{頭痛の有無}, \cdots)$

など）とし、それに対して風邪かどうかを $t$ （ $t=1$ なら風邪； $t=0$ なら風邪ではない）とします。

ここで考えるモデルは次のような条件付き確率で表されるモデルです：

$p(t=1|\phi) = \sigma(w^{T} \phi) := \frac{1}{1+\exp{(-w^{T}\phi)}}$

つまり、ある係数 $w$ があって、特徴 $\phi$ が得られたときに、クラス１（ $t=1$ ）である確率が $\sigma(w^{T} \phi)$ と表されるようなモデルです。ここで $\sigma$ はロジスティックシグモイド関数と呼ばれる関数で次のような関数になっています。

f:id:wakaba-mafin:20181217150657p:plain

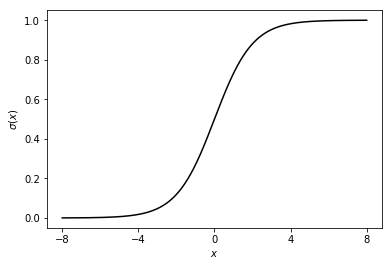
このようにロジスティックシグモイド関数 $\sigma(x)$ は $x$ が正のときには0.5より大きくて1に近い値になり、 $x$ が負のときには0.5より小さくて0に近い値になります。

つまり、ロジスティック回帰とは上式のモデルをデータから推定して、新たなデータに対してニクラス分類を行うというものです。

ロジスティック回帰の使い方

さて、ここではそのロジスティック回帰の使い方を述べます。ロジスティック回帰の使い方は大きく分けて２つのステップに分けられます。

得られているデータからモデルを学習
新しいデータに対してクラスを予測

上で述べた風邪の例であれば、ステップ１ではたくさんの患者さんを診察して、体温・熱・咳と風邪かどうかのデータを集めて、そこからモデル $p(t=1|\phi)$ に含まれる $w$ を推定します。そして、ステップ２では学習したモデルを使って、新たな患者さんの体温・熱・咳から風邪かどうかを判別するということを行います。

STEP1:既存のデータに対する学習

まずはステップ１から説明します。

今、データとして $\mathcal{D}=\{(\phi_i, t_i)\}_{i=1}^{N}$ （ $i$ に関して互いに独立）が得られているとしましょう。ここでやりたいことは $\mathcal{D}$ からモデル

$p(t=1|\phi,w) = \sigma(w^{T} \phi) := \frac{1}{1+\exp{(-w^{T}\phi)}}$

の $w$ を推定することです。この $w$ の推定の仕方はたくさんあるとは思いますが、ここではスタンダードな最尤推定を考えましょう。

最尤推定とは得られているデータが一番“尤もらしく”なるように $w$ を推定する方法です。つまり、尤度と呼ばれる

$p(t_1, \cdots, t_N|\phi_1, \cdots, \phi_N, w) = \prod_{i=1}^{N} p(t=1|\phi_i,w)^{t_i}(1-p(t=1|\phi_i,w))^{1-t_i},$

つまり、 $w$ を与えたときにモデルから今のデータが得られる確率を最大にすることによって、 $w$ を推定する方法です。

ま、このまま最大化してもいいのですが、 $N$ 個の掛け算をしていたり、指数の肩に $t_i$ が乗っかってるので面倒ですよね。そこで単調な関数 $\log$ をかまして簡単化しましょう。尤度の最大化は次の負の対数尤度の最小化に対応します：

$l(w|\mathcal{D}):=-\log p(t_1, \cdots, t_N|\phi_1, \cdots, \phi_N, w)$

つまり、

$l(w|\mathcal{D})= -\sum_{i=1}^{N} \left\{ t_i \log p(t=1|\phi_i,w) + (1-t_i) \log (1-p(t=1|\phi_i,w))\right\}$

ここまで来てしまえば最小化は簡単です。

f:id:wakaba-mafin:20181217155206p:plain

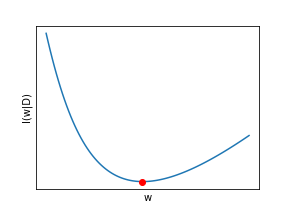
ここでは逐次的な最小化を考えて...

$w^{\rm new} = w^{\rm old} - \eta \nabla_w l(w|\mathcal{D}) = w^{\rm old} - \eta \sum_{i=1}^{N} \{p(t=1|\phi_i,w^{\rm old}) -t_i\} \phi_i$

と繰り返すことによって最小化を行います。最後の式変形は割と簡単に行うことができるので、ぜひやってみてください😆 $\eta$ は学習率と呼ばれるパラメータで、小さく固定したり、 $w$ の更新ごとに小さくしたり色んなやり方が提案されていますが、ここでは一番簡単な小さい値で固定ということにしておきます。これを最急降下法といいます。その他の手法については

qiita.com

postd.cc

あたりでまとめてくださっていますので、そちらをご参考にしていただければと思います！

そして、この繰り返しをある程度繰り返して $w$ を推定することができます。

STEP2:新たなデータに対する識別

$w$ が一度決まってしまえば、新たなデータに対する識別は簡単です。

今、新たな特徴として $\psi$ が得られたとしましょう。このとき、STEP1で求めた $w$ とモデルを使えば、

$p(t=1|\psi, w) = \sigma(w^{T} \psi)$

となります。これは、まさに新たに得られたデータに対して $t=1$ である確率を表しているので、ある閾値（一般的には0.5？）を超えていれば $\hat{t}=1$ ；下回って入れば $\hat{t}=0$ と識別すればOKです。この閾値については決定理論(Decision Theory)とも関わるのでまた違う記事で。

ロジスティック回帰の例

さて、ここまでロジスティック回帰についてうんちゃらかんちゃら述べてきました。

が、言葉だけではわかりにくいですよね？（私の説明能力が原因かもしれませんが💦）ということで、１つ例をとってPythonでロジスティック回帰を使ってみたいと思います！

今回使うライブラリはこちら。

# library
import numpy as np
import matplotlib.pyplot as plt

そして、データの生成。今回はこんな感じのデータにしてみましょう。

num = 1000
Phi = np.random.randn(num, 2)
T = np.array([1 if phi[0]-phi[1]>0 else 0 for phi in Phi], dtype=np.int32)
Phi += 0.5*np.random.randn(num,2)

plt.scatter(Phi[T==1, 0], Phi[T==1, 1], c="r", label="t=1", alpha=0.5)
plt.scatter(Phi[T==0, 0], Phi[T==0, 1], c="b", label="t=0", alpha=0.5)
plt.plot([-3,3], [-3,3], "k-", label="boundary")
plt.xlabel(r"$x$")
plt.ylabel(r"$y$")
plt.legend()
plt.show()

f:id:wakaba-mafin:20181217151253p:plain

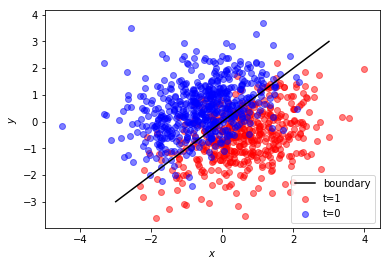
というわけで、学習。今回は学習率0.01くらいで1000回くらい回しましょう！

def sigmoid(a):
    return 1.0/(1.0 + np.exp(-a))

eta = 0.01
w = np.random.randn(2)
for n in range(1000):
    w = w - eta * Phi.T @ (sigmoid(Phi@w)-T)
    
print("result : ", w)

result :  [ 2.07706725 -2.14773041]

まま、 $(1,-1)$ の定数倍くらいの値が得られたのでよしとしましょう。

実際に新しいデータに対する判定は...

discrimination = np.array([[sigmoid(w[0]*x + w[1]*y) for x in np.linspace(-3,3,100)] for y in np.linspace(-3,3,100)])
plt.imshow(discrimination, aspect="auto", extent=(-3,3,-3,3), origin="bottom", cmap="bwr", interpolation="bilinear")
plt.colorbar()
plt.title("Prob(t=1)")
plt.xlabel("x")
plt.ylabel("y")
plt.show()

f:id:wakaba-mafin:20181217151318p:plain

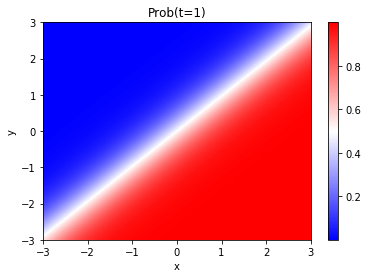
確かに、学習データに近い色合いになってますね！

実際に学習データとこれを重ね書きしてみて...

plt.imshow(discrimination, aspect="auto", extent=(-3,3,-3,3), origin="bottom", cmap="bwr", interpolation="bilinear")
plt.colorbar()
plt.scatter(Phi[T==1, 0], Phi[T==1, 1], c="r", label="t=1", alpha=0.5, edgecolors="k")
plt.scatter(Phi[T==0, 0], Phi[T==0, 1], c="b", label="t=0", alpha=0.5, edgecolors="k")
plt.plot([-3,3], [-3,3], "k-", label="genuine boundary")
plt.xlim(-3,3)
plt.ylim(-3,3)
plt.title("Prob(t=1)")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()

f:id:wakaba-mafin:20181217151339p:plain

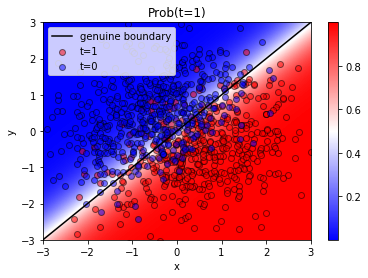
うん！いい感じ！

今回は自分で最急降下法組みましたけど...実はPythonのライブラリScikit-Learn使えばもっと簡単に実装できますけどね！

# library
from sklearn.linear_model import LogisticRegression

# Logistic回帰学習
lr = LogisticRegression().fit(Phi, T)

# 新たなデータに対する識別
num_of_data = 20
x_val, y_val = np.meshgrid(np.linspace(-3,3,num_of_data),np.linspace(-3,3,num_of_data))
t_disc = lr.predict(np.c_[x_val.ravel(), y_val.ravel()]).reshape(num_of_data, num_of_data)

# plot
plt.plot(x_val[t_disc==1], y_val[t_disc==1], "ro", label="t=1")
plt.plot(x_val[t_disc==0], y_val[t_disc==0], "bo", label="t=0")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()

f:id:wakaba-mafin:20181217151356p:plain

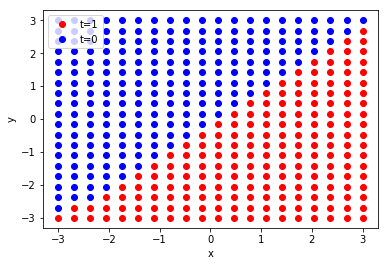
こちらの方が断然楽ですね笑

まとめ

今回はニクラス分類に対する１つのアプローチ：ロジスティック回帰をご紹介いたしました！ロジスティック回帰は得られているデータの特徴空間を線形に分類するような簡単な手法ですが、その簡便性より計算が高速だったりするのでよく用いられています。実際、ロジスティック回帰は最近流行っている機械学習・AIなどの簡単な一例になっています。

ぜひ今回の記事でクラス分類に興味を持っていただければ嬉しいです！

というわけで今回はここまで。

ご意見や間違いのご指摘・ご質問等ございましたら、ぜひコメントいただければ嬉しいです！

若葉の技術メモ